NPTEL Deep Learning Week 12 Assignment Answers 2025
1. During training a Variational Auto-encoder (VAE), it is assumed that P(z|x) ~ N(0,1) i.e., given
an input sample, the encoder is forced to map its latent code to NO, I). After the training is
over, we want to use the VAE as a generative model. What should be the best choice of
distribution from which we should sample a latent vector to generate a novel example?
a. N(0,1): Normal distribution with zero mean and identity covariance
b. N(1,1): Normal distribution with mean = 1 and identity covariance
c. Uniform distribution between [-1, 1]|
d. N(-1,1): Normal distribution with mean = -1 and identity covariance
Answer :- For Answers Click Here
2. When the GAN game has converged to its Nash equilibrium (when the Discriminator randomly
makes an error in distinguishing fake samples from real samples), what is the probability (of
belongingness to real class) given by the Discriminator to a fake generated sample?
a. 1
b. 0.5
c. 0
d. 0.25
Answer :-
3. Why is re-parameterization trick used in VAE?
a. Without re-parameterization, the mean vector of latent code of VAE encoder with tend towards zero
b. Sampling from a VAE encoder latent space is non-differentiable and thus we
cannot back propagate gradient during optimization using gradient descent
c. We need to re-parameterize Normal distribution over latent space to Bernoulli distribution
d. None of the above
Answer :-
4.
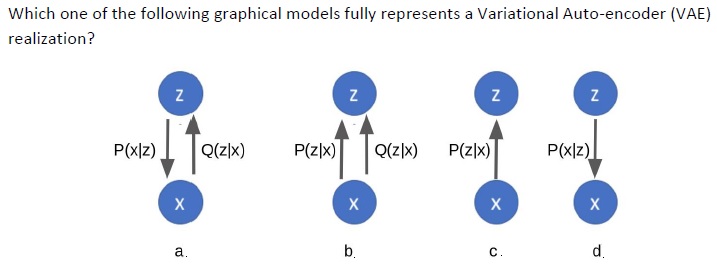
Answer :-
5.
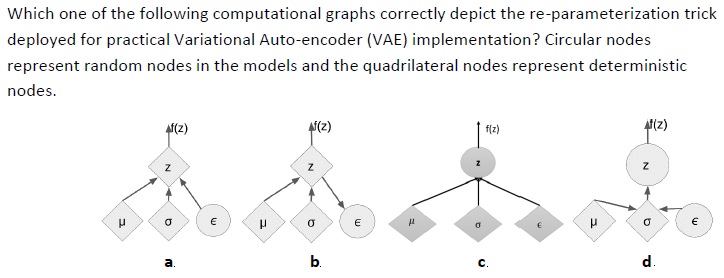
Answer :- For Answers Click Here
6.
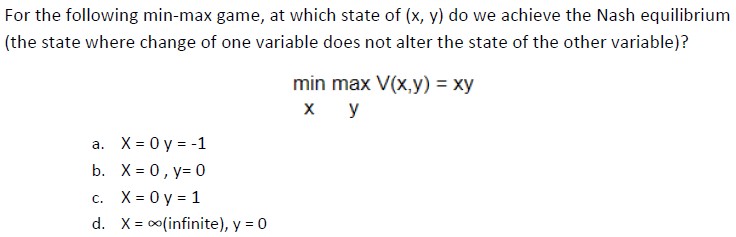
Answer :-
7. Which of the following losses can be used to optimize for generator’s objective (while training a
Generative Adversarial network) by MINIMIZING with gradient descent optimizer? Consider
cross-entropy loss,
CE(a, b) = – [alog(b) + (1-a)log(1-b)]|
and D(G(z)) = probability of belonging to real class as output by the Discriminator for a given
generated sample G(z).
a. CE(1, D(G(z)))
b. CE(1, -D(G(z)))
c. CE(1, 1 – D(G(z)))|
d. CE(1, 1 / D(G(z)))
Answer :-
8. While training a Generative Adversarial network, which of the following losses CANNOT be
used to optimize for discriminator objective (while only sampling from the distribution of
generated samples) by MAXIMIZING with gradient ASCENT optimizer? Consider cross-entropy
loss,
CE(a, b) = – [ a log(b) + (1-a)Iog(1-b)]
and D(G(z)) = probability of belonging to real class as output by the Discriminator for a given
generated sample, G(z) from a noise vector, z.
a. CE(1, D(G(z)))
b. -CE(1, D(G(z)))|
c. CE(1, 1 + D(G(z)))
d. -CE(1, 1 – D(G(z)))
Answer :-
9.

Answer :-
10.
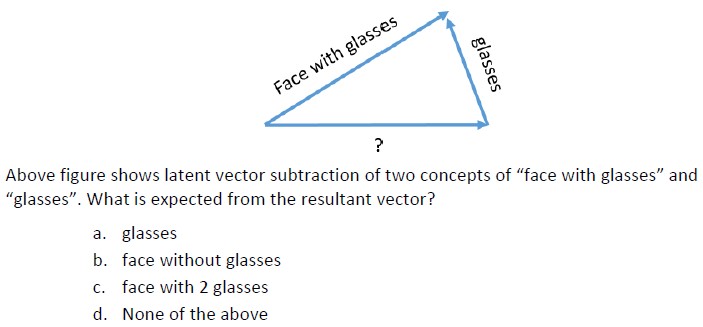
Answer :- For Answers Click Here


