NPTEL Introduction to Machine Learning Assignment Answers 2025
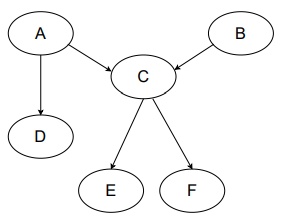
1. Consider the Markov Random Field given below. We need to delete one edge (without deleting any nodes) so that in the resulting graph, B and F are independent given A. Which of these edges could be deleted to achieve this independence?
Note: In each option, we only delete one edge from the original graph.

- AC
- BE
- CE
- AE
Answer :- For Answers Click Here
2. Consider the Markov Random Field from question 1. We need to delete one node (and also delete the edges incident with that node) so that in the resulting graph, B and C are independent given A. Which of these nodes could be deleted to achieve this independence?
Note: In each option, we only delete one node and its incident edges from the original graph.
- D
- E
- F
- None of the above
Answer :-
3. Consider the Markov Random Field from question 1. Which of the nodes has / have the largest Markov blanket (i.e. the Markov blanket with the most number of nodes)?
- A
- B
- C
- D
- E
- F
Answer :-
4. Consider the Bayesian Network given below. Which of the following independence relations hold?
- A and B are independent if C is given
- A and B are independent if no other variables are given
- C and D are not independent if A is given
- A and F are independent if C is given
Answer :-
5. In the Bayesian Network from question 4, assume that every variable is binary. What is the number of independent parameters required to represent all the probability tables for the distribution?
- 8
- 12
- 16
- 24
- 36
Answer :-
6. In the Bayesian Network from question 4, suppose variables A, C, E can take four possible values, while variables B, D, F are binary. What is the number of independent parameters required to represent all the probability tables for the distribution?
- 24
- 36
- 48
- 64
- 84
Answer :- For Answers Click Here
7. In the Bayesian Network from question 4, suppose all variables can take 4 values. What is the number of independent parameters required to represent all the probability tables for the distribution?
- 72
- 90
- 108
- 128
- 144
Answer :-
8. Consider the Bayesian Network from question 4. which of the given options are valid factorizations to calculate the marginal P (E = e) using variable elimination (need not be the optimal order)?
- ∑BP(B)∑AP(A)∑DP(D|A)∑CP(C|A,B)∑FP(E=e|C)P(F|C)
- AP(A)∑DP(D|A)∑BP(B)∑CP(C|A,B)∑FP(E=e|C)P(F|C)
- ∑BP(B)∑AP(D|A)∑DP(A)∑FP(C|A,B)∑CP(E=e|C)P(F|C)
- ∑AP(B)∑BP(D|A)∑DP(A)∑FP(C|A,B)∑CP(E=e|C)P(F|C)
- ∑AP(A)∑BP(B)∑CP(C|A,B)∑DP(D|A)∑FP(E=e|C)P(F|C)
Answer :-
9. Consider the MRF given below. Which of the following factorization(s) of P (a, b, c, d, e) satisfies/satisfy the independence assumptions represented by this MRF?
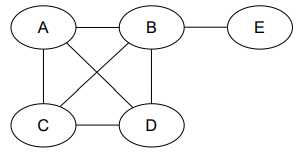
- P(a,b,c,d,e)=1Zψ1(a,b,c,d)ψ2(b,e)
- P(a,b,c,d,e)=1Zψ1(b)ψ2(a,c,d)ψ3(a,b,e)
- P(a,b,c,d,e)=1Zψ1(a,b)ψ2(c,d)ψ3(b,e)
- P(a,b,c,d,e)=1Zψ1(a,b)ψ2(c,d)ψ3(b,d,e)
- P(a,b,c,d,e)=1Zψ1(a,c)ψ2(b,d)ψ3(b,e)
- P(a,b,c,d,e)=1Zψ1(c)ψ2(b,e)ψ3(b,a,d)
Answer :-
10. The following figure shows an HMM for three time steps i = 1, 2, 3. Suppose that it is used to perform part-of-speech tagging for a sentence. Which of the following statements is/are true?
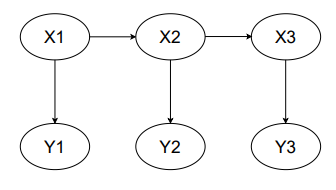
- The Xi variables represent parts-of-speech and the Yi variables represent the words in the sentence.
- The Yi variables represent parts-of-speech and the Xi variables represent the words in the sentence.
- The Xi variables are observed and the Yi variables need to be predicted.
- The Yi variables are observed and the Xi variables need to be predicted.
Answer :- For Answers Click Here


